Øvingsoppgaver i Matlab - For vidarekomne

.m files

Innheld litt meir avanserte øvingsoppgåver i Matlab
* Strukturert programmering - ulike løkker
* Avanserte plot
* Numerisk integrasjon
* Numerisk derivasjon
* Numerisk løysing av differensiallikninger

Contents

Oppgave 27 Funksjon med meir enn eit resultat

% funksjon som bereknar middelverdi og standardavvik
%
% Lage følgande fil, lagre som AMOstats
% Pass på at "current folder" er den katalogen der du har lagra fila
% Du kan sjekke dette i command window med kommanoden "pwd" (print working
% directory)
%       function [middel, stdavvik] = AMOstats(x)
%       % Beregne middelverdi og standardavvik av vektoren x
%       n=length(x);
%       middel=sum(x)/n;
%       stdavvik=sqrt(sum((x-middel).^2/(n-1)));
%
% prøv funksjonen med
x=[1.5 3.7 5.4 2.6 0.9 2.8 5.2 4.9 6.3 3.5];
[m s]=AMOstats(x);
m,s

n=length(x);
middel=sum(x)./n;
stdavvik=sqrt(sum((x-middel).^2./(n-1)));

m =

    3.6800


s =

    1.7662

Oppgave 28 Strukturert programmering - if-end

a = 2;
b = 3;
if (a<b)
    j = -1
end

j =

    -1

Oppgave 29 Structurert programmering - if-else-end

a = 4;
b = 3;
if (a<b)
    j = -1
elseif (a>b)
    j = 2
end

j =

     2

Oppgave 30 Structurert programmering - if-elseif-else-end

a = 4;
b = 4;
if (a<b)
    j = -1
elseif (a>b)
    j = 2
else
    j = 3
end
%

j =

     3

Oppgave 31 Structurert programmering - if-elseif-elseif-else-end

%  Alternative samanlikningsoperatorar (boolske operatorar)
%  "<",">", "<=", ">=", "=="
% Sjekk ut bruken av boolske operatorar (logiske operatorer)
a = 100;
if a == 10
      % dersom betingelsen er sann, skriv følgande til skjermen
   fprintf('Value of a is 10\n' );
elseif( a == 20 )
   % dersom |elseif| betingelsen er sann:
   fprintf('Value of a is 20\n' );
elseif a == 30
   % dersom neste |elseif| betingelse er sann:
   fprintf('Value of a is 30\n' );
else
   % dersom ingen av betingelsane er sanne'
   fprintf('None of the values are matching\n');
   fprintf('Exact value of a is: %d\n', a );
end

None of the values are matching
Exact value of a is: 100

Oppgave 32 Structurert programmering - if-else-end

age = 20;
if age < 18
   disp('You are not allowed to buy alcohol')
elseif age >= 18 & age < 20
   disp('You can buy alcohol below 22%')
else
   disp('You can buy all sorts of alcohol')
end

You can buy all sorts of alcohol

Oppgave 33 Strukturert programmering - Bruk av for ... end (1)

	for i = 1:4
        i
    end

i =

     1


i =

     2


i =

     3


i =

     4

Oppgave 34 Bruk av for ... end (2)

Computes the product of all the integres fom 1 to n

n=6;
x = 1;  % in order to provide the correct result of 0!
for i = 1:n
    x = x*i;
end
fout = x

fout =

   720

Oppgave 35 Bruk av for ... end (3)

for a = 10:20
  fprintf('value of a: %d\n', a);
end

value of a: 10
value of a: 11
value of a: 12
value of a: 13
value of a: 14
value of a: 15
value of a: 16
value of a: 17
value of a: 18
value of a: 19
value of a: 20

Oppgave 36 Bruk av for ... end (4)

for a = 1.0: -0.1: 0.0
   disp(a)
end

     1

    0.9000

    0.8000

    0.7000

    0.6000

    0.5000

    0.4000

    0.3000

    0.2000

    0.1000

     0

Oppgave 37 Bruk av for ... end (5)

for a = [24,18,17,23,28]
   disp(a)
end

    24

    18

    17

    23

    28

Oppgave 38 Strukturert programmering - Bruk av While-løkke

h = 0.001;
x = 0:h:2;
y = 0*x;
y(1) = 1;
i = 1;

size(x)
max(size(x))

while(i<max(size(x)))
   y(i+1) = y(i) + h*(x(i)-abs(y(i)));
   i = i + 1;
end
plot(x,y,'go')
plot(x,y)

ans =

           1        2001


ans =

        2001

Oppgave 39 Lag eit litt avansert plot

t=0:0.1:10;        % variable definition
y1=sin(t);         % Function 1
y2=cos(t);         % Function 2
plot(t,y1,'r',t,y2,'b--');  % Plot dei to funksjonane

title('Sin and Cos');	% Gi plottet ein tittel
legend('sin','cos')	% Legg til forklaring på kvar av dei to kurvene
% ------- Legg på litt meir tekst på plottet
xlabel('time')	% set namn på x-aksen
ylabel('sin & cos')	% set namn på y-aksen
grid on		% Legg til grid på figuren
axis square		% La forma på figuren vere kvadratisk

x=[1.6*pi;1.4*pi];   % Definer 2 x-koordinatar
y=[-0.35; 0.65];       % Definer to tilhøyrande y-koordinatar
s=['sin(t)';'cos(t)']; % definer ein tekststreng
text(x,y,s);	% Plasser tekststrengen i det definerte punktet (x,y)

Oppgave 40 Lag eit plot basert på tilpasning av data

x=[14.2 16.4 11.9 15.2 18.5 22.1 19.4 25.1 23.4 18.1 22.6 17.2];
y=[215 325 185 332 406 522 412 614 544 421 445 408];

coeff = polyfit(x,y,1);
y_fit = polyval(coeff,x);

plot(x,y,'r+',x,y_fit)
grid on
xlabel('x-data')
ylabel('y-data')
title('Basic curve-fitting')
legend('Original data','Line of best fit','Location','SouthEast')

Oppgave 41 Lage diverse 3D plot med funksjonen plot3

t=0:pi/50:10*pi;
plot3(sin(t),cos(t),t, 'r.')
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('3D helix')

Oppgave 42 Fleire 3D plot

% Ein helix frå funksjonane
%
% x = sin(t/2c) cos(t)
% y = sin(t/2c) sin(t)
% z = cos(t/2c)
%
c=5;t=0:pi/10:10*pi;
x = sin(t./(2*c)).*cos(t);
y = sin(t./(2*c)).*sin(t);
z = cos(t./(2*c));
plot3(x,y,z)
%

Oppgave 43 Ei sinusbølge på ei kule

% x=cos(t)*sqrt(b^2-c^2*cos^2(at))
% y=sin(t)*sqrt(b^2-c^2*cos^2(at))
% z=c*cos(at)
a=10;b=1;c=0.3;t=0:pi/100:2*pi;
x=cos(t).*sqrt(b^2-c^2*cos(a.*t).^2);
y=sin(t).*sqrt(b^2-c^2*cos(a.*t).^2);
z=c.*cos(a*t);
plot3(x,y,z)
%

Oppgave 44 Lage eit 3D plot med meshgrid som base

% Første må du lage eit grid av (x,y) verdiar, deretter
% skal du plotte funksjonen
%
%  $z = c \cdot \sin(2 \pi a \sqrt{x^2+y^2}$
x=linspace(-1,1,50);
y=x;
a=3;c=0.5;
[xx, yy] = meshgrid(x,y);
z = c*sin(2*pi*a*sqrt(xx.^2+yy.^2)); 
surf(xx,yy,z)
colorbar
xlabel('x')
ylabel('y')
zlabel('z')
title('f(x,y)=c sin(2 \pi a \surd(x^2+y^2))')
figure;

% Så ein liknande variant men med |mesh| istaden for |surf|

mesh(xx,yy,z)
colorbar
xlabel('x')
ylabel('y')
zlabel('z')
title('f(x,y)=c sin(2 \pi a \surd(x^2+y^2))')

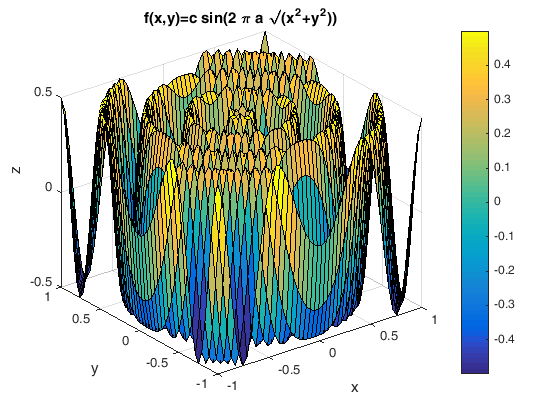
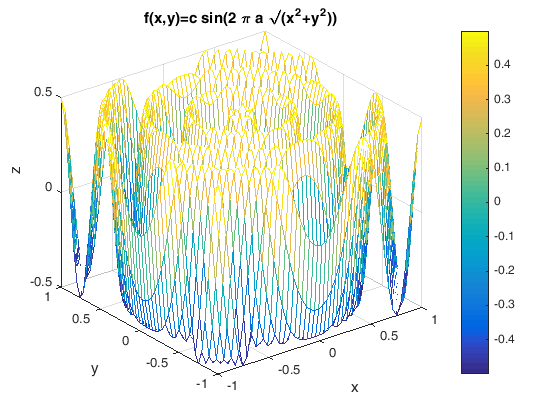
Oppgave 45 Avansert 3D plot ved å bruke meshc

% Kurva z=exp(-sqrt(x^2+y^2)*cos(4x)*cos(4y)) skal plottast
% Max og min på kurva skal identifiserast
%
%  Denne oppgava brukar avanserte funksjonar som kun er med her
%  for å illustrere noko av dei opsjonane som finnest i Matlab
[x, y] = meshgrid(linspace(-1, 1, 31));
z2 = exp(-sqrt(x.^2+y.^2)).*cos(4*x).*cos(4*y);
meshc(x, y, z2);
xlabel('x');
ylabel('y');
zlabel('z');
title('z = e^{-(x^2+y^2)^{0.5}} cos(4x) cos(4y)');
MinVal = min(min(z2))
MaxVal = max(max(z2))
XatMin = x(find(z2 == MinVal))
YatMin = y(find(z2 == MinVal))
XatMax = x(find(z2 == MaxVal))
YatMax = y(find(z2 == MaxVal))

%

MinVal =

   -0.4699


MaxVal =

     1


XatMin =

   -0.7333
         0
         0
    0.7333


YatMin =

         0
   -0.7333
    0.7333
         0


XatMax =

     0


YatMax =

     0

Oppgave 46 Alternativt plot ved bruk av r og theta

[r, theta] = meshgrid(linspace(0, 1.7, 60),linspace(0, 2*pi, 73));
x = r.*cos(theta);
y = r.*sin(theta);
z = exp(-r).*cos(4*x).*cos(4*y);
meshc(x, y, z);
x('x');
y('y');
z('z');
%

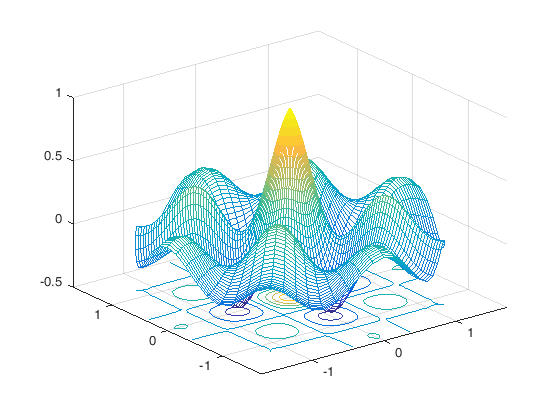
Oppgave 47 Variant ved å bruke surfc

surfc(x, y, z);
shading interp
xlabel('x');
ylabel('y');
zlabel('z');

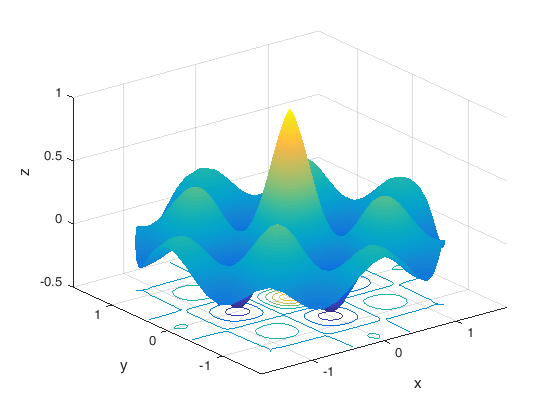
Oppgave 48 Bruk av funksjoner

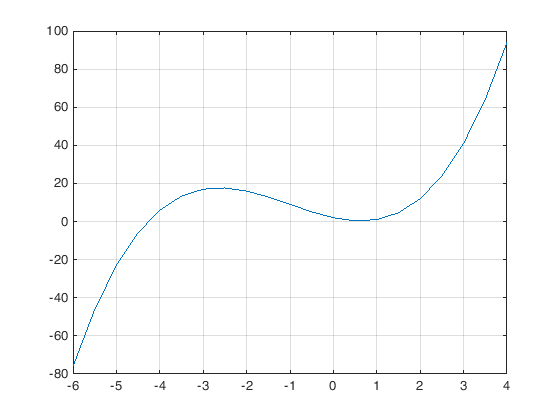
Du må lagre ei eiga fil som du kallar my_func.m Fila skal ha følgande innhald function y = my_func(x) y=x.^3+3.*x.^2-5.*x+2

x=-6:0.5:4;
y = x.^3+3.*x.^2-5.*x+2;
plot(x,y)
grid
%y=my_func(x);
% Lag så ei eiga fil som heiter trapes1.m
% og har følgande innhald
%       function area=trapes1(f,a,b)
%       ya=feval(f,a);
%       yb=feval(f,b);
%       area=(b-a)*(ya+yb)/2;
% Funksjonen 'feval(f,a)' er ein innebygd funksjon som
% reknar ut funksjonen 'f' med argumentet 'a'

% Prøv så følgande program eit par gongar
area=trapes1('my_func',2,4)
area=trapes1('my_func',-4,-2)

% Du kan kontrollere svara
ya=my_func(2);yb=my_func(4);
areal=(ya+yb)/2*(4-2)

ya=my_func(-4);yb=my_func(-2);
areal=(ya+yb)/2*(-2+4)

area =

   106


area =

    22


areal =

   106


areal =

    22

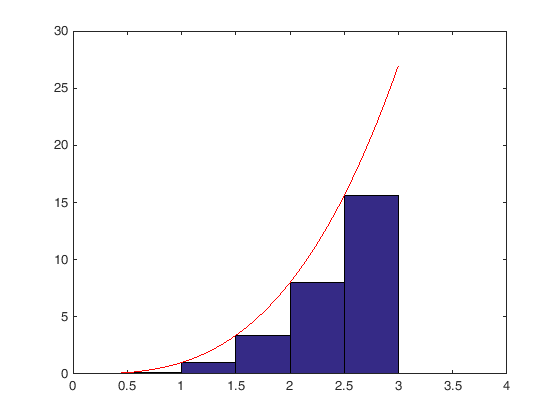
Oppgave 49 Numerisk integrasjon - ein sum av nedre rektangel

clf
h=0.5;
x1=0:h:3-h;
y1=x1.^3;
bar(x1+h/2,y1,1)  % Plot av rektangel, nedre ende

hold on
x=0:h/10:3;
y=x.^3;
plot(x,y,'r-')     % Plot av den kontinuerlige funksjonen
axis([0 4 0 30])
hold off

% Arealberekningar
n=length(x1);
A=0;
for i = 1:n
    A=A+y1(i)*h;
end
A

A =

   14.0625

Oppgave 50 Numerisk integrasjon - sum av øvre rektangel

clf
h=0.5;
x1=h:h:3;
y1=x1.^3;
bar(x1-h/2,y1,1)  % Plot av rektangel, øvre ende

hold on
x=0:h/10:3;
y=x.^3;
plot(x,y,'r-')     % Plot av den kontinuerlige funksjonen
axis([0 4 0 30])
hold off

% Arealberekningar
n=length(x1);
A=0;
for i = 1:n
    A=A+y1(i)*h;
end
A

A =

   27.5625

Oppgave 51 Numerisk integrasjon - sum av midtre rektangel

clf
h=0.5;
x1=h:h:3;
y1=(x1-h/2).^3;
bar(x1-h/2,y1,1)  % Plot av rektangel, øvre ende

hold on
x=0:h/10:3;
y=x.^3;
plot(x,y,'r-')     % Plot av den kontinuerlige funksjonen
axis([0 4 0 30])
hold off

% Arealberekningar
n=length(x1);
A=0;
for i = 1:n
    A=A+y1(i)*h;
end
A

A =

   19.9688

Oppgave 52 Løyser diff. likn. y'=x^2-y^2, y(0)=1 ved å bruke Eulers metode

h = 0.1;
x = 0:h:2;       % Definere x-variabelen

y = 0*x;
y(1) = 1;
n=length(x);     % Finne lengda på x-vektoren

for i=2:n,
  y(i) = y(i-1) + h*(x(i-1)^2 - y(i-1)^2);
end

plot(x,y)
plot(x,y,'go')
plot(x,y,'go',x,y)

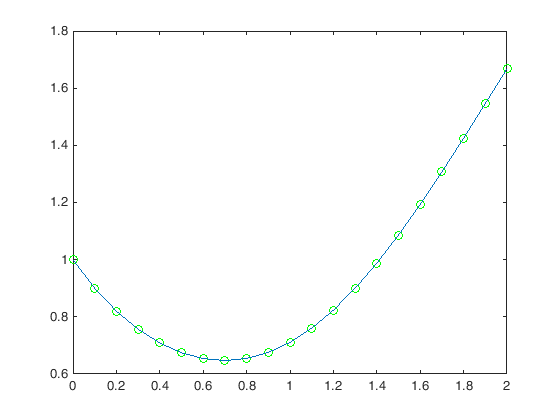
Oppgave 53 Matlab program - Strekkhopppar med Eulers metode

clear all
g=9.81;m=80;cd=0.25;
t0=0;tend=20;dt=0.5;vi=0;
t=t0:dt:tend;

% The analytic solution
vel=sqrt(g*m/cd)*tanh(sqrt(g*cd/m)*t);

% The numerical solution
n=(tend-t0)/dt;
v=vi;
V(1)=v;
for i=1:n
    dv=g-(cd/m)*v*abs(v);
    v=v+dv*dt;
    V(i+1)=v;
end

% Plotting of results
plot(t,vel,t,V,'r.')
grid
title('Velocity for the bungee jumper')
xlabel('time (s)')
ylabel('velocity (m/s)')
legend('analytical','numerical',2)

Published with MATLAB® R2014b